

|

Cycle Length Determination
Once you know the total cycle length, you can subtract the length of the
amber and all-red periods from the total cycle length and end up with the total time
available for green signal indications. Efficiency dictates that the cycle length should
be long enough to serve all of the critical movements, but no longer. If the cycle is
too short, there will be so many phase changes during an hour that the time lost due to
these changes will be high compared to the usable green time. But if the cycle is too
long, delays will be lengthened, as vehicles wait for their turn to discharge through the
intersection. Figure 1 provides a graphical portrayal of this phenomenon.
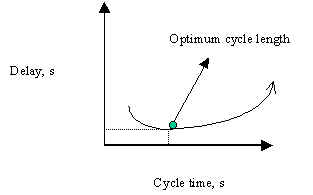
Figure 1: Cycle Length versus Delay
Several methods for solving this optimization
problem have already been developed, but Webster’s equation is the most
prevalent. Webster's equation, which minimizes intersection delay, gives the
optimum cycle length as a function of the lost times and the critical flow
ratios. Many design manuals use Webster's equation as the basis for their design and
only make minor adjustments to suit their purposes. Webster's equation is shown below.
Co= 1.5L + 5
1 - S (V/s)
Where:
Co = Optimum cycle length (sec)
L = Sum of the lost time for all phases, usually taken as the sum of the intergreen
periods (sec)
V/s = Ratio of the design flow rate to the saturation flow rate for the critical approach
or lane in each phase
After you have calculated the optimum cycle length, you should increase it to the
nearest multiple of 5. For example, if you calculate a cycle length of 62 seconds,
bump it up to 65 seconds. Once you have done this, you are ready to go. If you
know the intergreen times for all of the phases, you can then calculate the total
available green time and allocate it to the various phases based on their critical
movements. (See the module entitled green split determination.)
|