
Queuing Theory
Queuing theory provides the design engineer with a traffic flow model
that can be used in the design of signalized intersections. Consider a simple
situation in which traffic is arriving at an intersection approach in a uniform manner,
with equal and constant headways between each vehicle. This constant flow rate is
shown in the figure below.
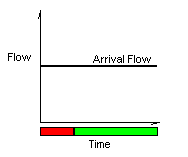
Figure 1: Constant Arrival Flow
During the red interval for the approach, vehicles cannot depart from the intersection
and consequently, a queue of vehicles is formed. When the signal changes to green,
the vehicles depart at the saturation flow rate until the standing queue is
cleared. Once the queue is cleared, the departure flow rate is equal to the arrival
flow rate. Figure 2 illustrates this behavior..
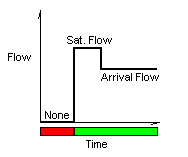
Figure 2: Departure Flow or Service Flow versus Time
The combined effect of the arrival and departure flow rates is illustrated by graphing
queue length versus time. During the red interval, the line of vehicles waiting at
the intersection begins to increase. The queue reaches its maximum length at the end of
the red interval. When the signal changes to green, the queue begins to clear as
vehicles depart from the intersection at the saturation flow rate. See the figure below.
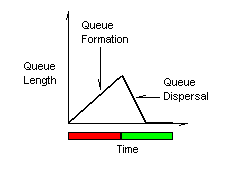
Figure 3: Queue Length versus Time
There is another graph that allows us to glean even more information from our
model. Imagine a plot where the x-axis is time and the y-axis contains the vehicle
numbers according to the order of their arrival. Vehicle one would be the first
vehicle to arrive during the red interval and would be the lowest vehicle on the
y-axis. If you were to plot the arrival and departure (service) times for each
vehicle, you would get a triangle as shown in figure 4 below.
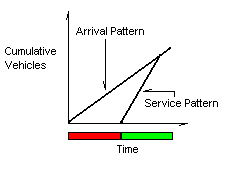
Figure 4: Vehicles versus Time
While this graph may not seem informative at first, a second look reveals its
insights. For a given time, the difference between the arrival pattern and the
service pattern is the queue length. For a given vehicle, the difference between the
service pattern and the arrival pattern is the vehicle delay. In addition, the area of the
triangle is equivalent to the total delay for all of the vehicles. See figure 5
below.
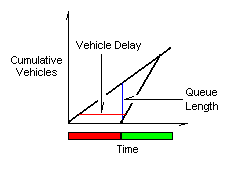
Figure 5: Graph Properties
As you would expect, the first vehicle to be stopped by the red signal experiences the
most delay. In addition, the queue is longest just before the green interval
begins. Queuing theory provides a foundation for the optimization of signal timing.
|