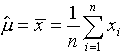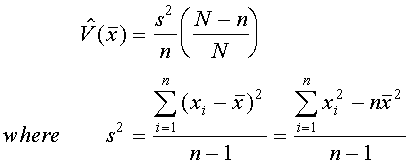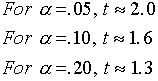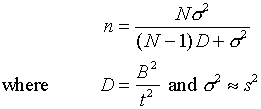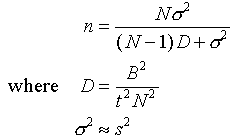Wlf 543
E. O. Garton
1. Objective: Take a sample from the population, measure some characteristic on each of the sampled units, and use this information to estimate (infer) the characteristic in the entire population.
2. Simple random sampling is the most basic sampling procedure to draw the sample.
3. Simple random sampling forms the basis for many of the more complicated sampling procedures.
4. Simple random sampling is easy to describe but is often very difficult to carry out in the field where there is not a complete list of all the members of the population.
DEFINITION: A simple random sample is a sample of size n drawn from a population of size N in such a way that every possible sample of size n has the same chance of being selected.
5. Note that this definition requires that we know the population size N.
ASSUMPTIONS FOR SIMPLE RANDOM SAMPLING
Simple random sampling is one form of the general set of sampling procedures referred to as probability sampling. Probability sampling procedures must meet 4 criteria (Chochran, 1977:9):
1. We can define the set of distinct samples which the procedure is capable of selecting.
2. Each possible sample has assigned to it a known probability of selection.
3. We select one of the samples by a random process in which each sample receives its appropriate probability of being selected.
4. The method for computing the estimate must lead to a unique estimate for any specific sample.
For any sampling procedure of this type we can calculate the frequency distribution of the estimates that it generates if repeatedly applied to the same population and therefore determine bias and variance of the estimator. In general we do not assume that the underlying population follows a normal distribution, but in order to calculate bounds and confidence intervals from single samples it may be useful to assume that the estimates follow a normal distribution. This assumption will be appropriate for large sample sizes but will be problematic for small sample sizes drawn from highly skewed populations. Cochran (1977:42) suggested the "crude rule" for positively skewed distributions that n should be greater than 25G12 where G1 is Fisher's measure of skewness. Alternately Tchebysheff's theorem states that at least 75% of the observations for any probability distribution will be within 2 standard deviations of their mean (Scheaffer et al., 1986:16).
Taking all of this together, we can state the following assumptions for simple random sampling:
1. The sample units included in the sample must be selected in a truly random manner from the population (a random, independent sample).
2. The estimator must follow a normal distribution for the bound and confidence interval to give correct coverage (large sample or normal population).
3. Failing 2 above, the bound calculated as 2 times the standard error of the estimator will include the true value for the population parameter in atleast 75% of the cases.
DRAWING A SIMPLE RANDOM SAMPLE
1. Two commonly used "random" sampling procedures do not yield simple random samples:
Haphazard sampling:
Representative sampling:
2. True random samples virtually always involve the use of random numbers from a random number table or an algorithm on a computer.
3. Drawing a simple random sample is accomplished by making a complete list of all the elements in a population, assigning each a number and then drawing a set of random numbers which identifies n members of the population to be sampled. Note that any random number is rejected which is a repeat of a previously sampled number so that each element of the population is sampled only once. This is termed sampling without replacement. The alternative of sampling with replacement is also possible and it useful in some situations.
4. EXAMPLE: Suppose that we wanted to sample a stream to estimate the mean number of fish per pool. We could travel along the stream from its mouth to its headwaters identifying the pools and assigning each pool a number. Then we could pick n random numbers from a random number table and sample the pools corresponding to those numbers.
5. An alternative way to use random numbers to select samples if you have access to a computer is the following:
A. Enter a list of the elements of your population into a spreadsheet or database or statistical data set.
B. Assign each element a random number.
C. Sort the elements by the random numbers.
D. Print out the sorted list.
E. The first n elements on your list consist of a random sample of size n from your population.
An advantage of this approach is that if you later decide to increase your sample size you can simply add the next couple of observations on your sorted list, or you can decrease your sample size by dropping off the last couple of samples on your list. In reality we have to make these kinds of adjustments to our sampling as we proceed in a typical study.
ESTIMATING THE POPULATION MEAN ![]()
1. Estimated Mean:
2. Estimated Variance of Mean:
3. Bound on the error of estimation (B):
Note that the t in the equation for the bound is a Student's t value for n-1 d.f. at the
level of significance. In most cases the following approximations are reasonable:
4. Confidence Interval:
5. Sample size:
Note: Use t=2 for 95% Bound etc.
ESTIMATING THE POPULATION TOTAL ![]()
1. Estimate of Total:
2. Estimated Variance of Total:
3. Estimated Bound on Total:
4. Sample Size:
Note: Use t=2 for 95% Bound etc.