Measuring density with plots & quadrats

What is a Quadrat?

A quadrat is typically a square frame constructed of plastic or pvc pipe, metal rod, or wood that is placed directly on top of the vegetation. Quadrats are also commonly called "plots."

Quadrats do not have to be square but their area must be known. Other quadrat shapes commonly include circles and rectangles.

Square quadrats can be any size. Common sizes include: 25 by 25 cm, 50 by 50 cm, 1 by 1 m and similar sizes in feet. Quadrats are used in many different scientific disciplines from vegetation assessment to archeological investigations. Quadrats are required for estimating several vegetation attributes including:

• Density - for counting the number of objects within the unit area of the quadrat.

• Biomass - achieved by "clipping" all the material of a given type (e.g., grass, shrub or forb) or species within a quadrat.

• Cover - often accomplished by estimating the area of a quadrat that is covered by a plant's canopy.

• Frequency - the proportion of quadrats in which a species occurs is called frequency, thus quadrats are required to estimate plant frequency.

Design of Quadrat-based Sampling

Four properties of a monitoring protocol are essential to consider before starting a sampling protocol using quadrats (Bonham 1989). They are:

1. What is the distribution of the plants across the landscape under assessment?

• Is the distribution of plants clumped and variable, heterogeneous, across the landscape?
• Or, are plants rather evenly, homogeneously, distributed across the landscape?
• Do the features of interest occur in linear strips, clumps, and what average area does one individual occupy?

2. What size quadrat should be selected?

• In selecting an appropriate quadrat size, we need to ensure that the quadrats are big enough to contain at least one plant of interest and should include enough plants to get a good estimate of density.
• Conversely, the quadrat needs to be small enough that the count can be conducted in a reasonable amount of time. In other words, you don't want to measure hundreds of individuals per quadrat.

Rules of Thumb for Quadrat Size:

• A quadrat is too large if the 2 most abundant species are found in every plot.
• A quadrat is too small if the most abundant species is not found in a majority of the plots.
• If more than 5% of sampling units have none of the plants of interest, increase the plot size.

Quadrat Size Depends on Plant Size:

• The larger the average sized plant the larger the necessary frame.
• A plot should be larger than the average-sized plant and larger than the average space between plants.
• It is difficult to sample plants of different life forms (i.e., shrubs and grasses) with the same plot frame. Therefore, nested techniques are often used where shrubs are measured with one plot (e.g., a longbelt transect) and herbaceous plants are measured with a separate, often smaller, plot.
• Select the size of quadrat based on species of greatest interest.

Perimeter to Area Ratio:

• The perimeter:area ratio decreases as plot size increases.
• If borderline decisions (i.e., is a plant in or out of plot) are difficult to make, then select a plot size that reduces the perimeter:area ratio.

The Bottom Line:

• Sparse vegetation requires larger quadrats than dense vegetation.
• Uniform vegetation requires fewer and smaller quadrats than diverse and heterogeneously distributed vegetation.

3. What shape of quadrat should be selected?

Many quadrat shapes exist for vegetation assessment -- from squares to rectangles to circles.

Rectangle --

• More likely to cut across plants or clumps of plants rather than be completely occupied by plants. So, generally best for "clumped" vegetation.
• Rarely completely occupied by bare spaces.
• Often have lower variance than squares or circles.
• Can reduce plot to plot variability in sparsely vegetated communities.
• Easier to estimate % cover than in circles or squares.

Elongated rectangles have often been shown to work effectively in ecological studies (Bonham 1989; Elzinga et al. 2001), because vegetation frequently occurs in clumps. Belt transects are rectangular in shape, where the "long" end is very much longer than the short end. Belt transects, sometimes called strip quadrates, differ from line transects as they have a larger and specifically defined width. A line transect is a narrow line (< 1 inch wide) stretched across a plot and it is not a "quadrat" because it has no area. Whereas a belt transect is several feet or meters wide and is a quadrat of sorts.

Square --

• Greater perimeter:area ratio than circles but less than rectangles.
• Most typically used to estimate frequency because presence/absence is easy to estimate.
• Squares are easier to estimate % cover than circles but not as easy as rectangles.

Circle --

• Less perimeter (per area) than square or rectangle.
• Often used in clipping because perimeter decisions are difficult to make when clipping.
• Reducing perimeter:area ratio is also good in communities with large sod-forming plants.

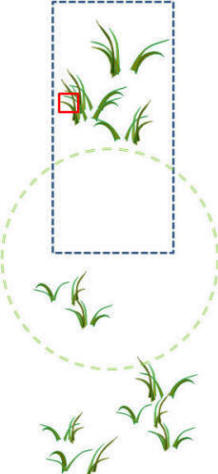
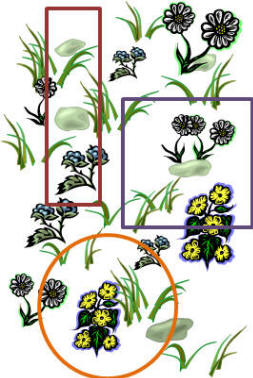
In the figure to the right, the red square would clearly be too small a quadrat because it is too small to capture even a single individual. Likewise, the green circle in this example although is big enough to capture >1 individual its shape is not optimal in capturing the density of these clumped plants. In this example. the elongated rectangle is the most appropriate quadrat as both a representative number are sampled and the shape captures the typical arrangement of plants.

4. How many observations are needed to accurately estimate the density of the species?

The number of observations needed is determined by the sampling protocol. However, most studies seek to have enough plots so that the standard error of the mean is about 10% or less. As variability in plant community increases:

• Necessary sample size increases

• Plot size increases

• Need for stratification increases

The Size-Variability Trade Off:

• Small quadrats (or plots) tend to have higher variability or express greater differences from plot to plot.
• Small plots are usually faster to read.
• But, the number of plots you must examine depends on variability.  The more variation among plots, the more plots you need to estimate.
• Therefore, there is a trade-off between number needed and quadrat size.

Sources of Uncertainty

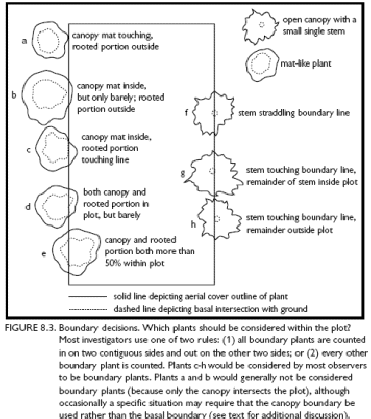One of the main sources of error in quadrat based sampling occurs when deciding whether an individual is within or outside the quadrat frame. These types are errors are called "boundary decisions" and protocols should be discussed to ensure consistent decisions (Elzinga et al. 1998). For example, would you include a species that entered the quadrat or just those species with roots in the quadrat. What then happens with species that roots cross the quadrat but terminate outside it? Can you achieve this assessment without damaging the plant? A further common source of error is due to differences in observers opinion. Again this can be minimized by having clear consistent standards. For more details on boarder decision study figure above and text in Elzinga et al. 1998.

Summary Questions

1. In the following 6 "quadrats" of plants, what is the average density (and standard error) of "white daisy" plants in plant/m²?
   Assume that each quadrat is 50 by 50 cm. The "white daisy" plants are:

»»Click here to see answer and calculations

Advanced Questions:

1. What size and shape of quadrat would you use to measure (a) the density of big sagebrush and (b) the density of western juniper in great basin rangelands?