WLF 448: Fish & Wildlife Population Ecology

Lab 10: Population Growth in Limited Environments

Fall 2004

  I. Introduction to Logistic Growth

A. Population growth can obey the exponential equation only under special circumstances and for short periods of time. In most cases:

1. As N increases, resources become limited and intraspecific competition can become important.

2. As N increases, density-dependent factors negatively affect mortality, survival, and/or birth rates, which lead to a decrease in population growth rate.

3. Population growth rates are not constant.

B. General features of the logistic-growth model:

1. In the beginning, population growth is nearly exponential, with increases close to r_max.

2. There is a constant linear decrease in the growth rate (r) as population size increases.

3. Population size plateaus and fluctuates around some mean.

4. The resulting logistic growth curve is S-shaped (sigmoid curve) and has 3 important characteristics:

   • The curve has an upper asymptote called the carrying capacity (K). This is the maximum population size at which dN/dt = 0.

   • Deceleration in population growth is smooth as it approaches K; thus, when the curve is cut in half, the upper and lower halves are mirror images. The point where you could cut the curve in half is called the inflection point, and it occurs at K/2.

   • The maximum number of individuals being "added" to the population per unit of time (dN/dt) occurs at N = K/2. Theoretically, this point on the growth curve is the population level at which one could manage for Maximum Sustained Yield (MSY).

C. Assumptions (Krebs 1972:194-195):

1. Population starts with a stable-age distribution.

2. Density is measured in appropriate units (i.e., individuals are equal versus age-specific differences).

3. There is a real attribute of the population corresponding to r.

4. The relationship between density and rate of increase per individual is linear.

5. The relationship between density and the rate of increase operates instantaneously without any time lags.

6. Carrying capacity is constant.

7. The population is large.

The logistic equation provides a relatively good fit to many case histories of population growth observed in the lab and field; however, it is just a model and contains several oversimplifications. Nevertheless, the logistic model provides a good introduction to more complex subjects such as density-dependence and mean population level.

II. Logistic Growth Models

A. Overlapping generations with discrete breeding periods

1. Finite rate of increase (lambda) is NOT a constant anymore but a function of current population size:

lambda = - B(N_t-K) + 1

                Note: This is the equation of a line y = mx + b

		where Nt = current population size. 

                 K = equilibrium population size (at K, lambda = 1). 

                 B = how fast growth declines with increasing density (rate of change in lambda)

2. Population size can be calculated as:

N_t+1 = N_t (- B(N_t-K) + 1)

3. Predicting the behavior of the population as it approaches equilibrium (K):

L = BN_eq

• If L < 1.0, then population will approach N_eq smoothly.

• If 1.0 < L < 2.0, then oscillations of decreasing amplitude around N_eq.

• If 2.0< L < 2.57, then stable, cyclic oscillations around N_eq .

• If L > 2.57, then population will fluctuate chaotically.

Biological Significance: If a population has even a moderate net-reproductive rate, and if it has a density-dependent reaction, which even moderately overcompensates, then far from being stable, it may fluctuate in numbers without any extrinsic factor acting (Begon and Mortimer 1986:49).

Note:  This population behavior is very similar to the behavior of a famous model used extensively in fisheries population studies, the Ricker model.  This model was explored in some depth by Robert May (1974) in a famous paper in Science (186:645-647).  He pointed out that as the populations maximum rate of increase went above 2 the population behavior first became cyclic, showing different length periods, then above 2.57 it showed chaotic population changes.  

You can explore this model in the lab on the Populus program.

4. Time lags (Birth Pulse Model).

• Assume that lambda at time t is dependent on the population size at time t. However, lambda at time t may in fact be dependent on the population size at some previous time denoted N_t-L, where L = the time lag. Lambda can be calculated as:

lambda_t = [1-B(N_t-L - N_eq)]

and the population at time t+1 is:

N_t+1 = N_t [1 - B(N_t-L - N_eq)] .

B. Overlapping generations with continuous breeding (birth flow)

1. If K = maximal value of N ("carrying capacity") then:

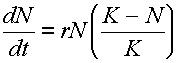
or

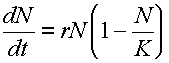
where dN/dt = rate of population increase per unit of time. 

          K = the maximum number of individuals that the given
              environment can support, i.e., the upper limit of
              population growth. 

Basically, this equation states that:

2. Population size at any future time can be calculated as:

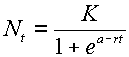
where "a" is a constant =

Note: the basic logistic equation, with no time lags, results in a population always approaching K with exponential damping .

3. Time lags (birth-flow model)

• If a time lag is involved, then the rate of change of population size is:

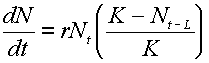
where L = lag time

• The introduction of time lags into simple models of population growth causes the smooth, stable asymptote of the logistic curve to be replaced by one of 3 alternatives (Krebs 1972:203):

• a converging oscillation toward equilibrium,

• a stable oscillation about the equilibrium level, or

• a divergent oscillation that is unstable and leads to extinction of the population.

• Longer time lags in general produce more numerical instability.

Note: Time lags, high reproductive rates, and highly overcompensating density-dependence (either alone or in combination) are capable of provoking all types of fluctuations in population density, without invoking any extrinsic factor (Begon and Mortimer 1986:50).

Program POPULUS - instructions will be given in lab.

POPULUS is a population biology simulation program.  It can be obtained from K:\WLF\448\2004\Lab2004\Populus5.3.  Copy the entire Populus5.3 folder and its contents onto your zip disk or personal H: drive.  Navigate to your Populus5.3 folder and double click on Populus under the Populus Files folder to start the POPULUS program.  You can learn more about Populus by reading the 'readme' file under the Populus5.3 folder or you can look under Help in the Populus program.

III. Problem Set

IV. Selected References

• Begon M., and M. Mortimer. 1986. Population ecology: A unified study of animals and plants. Blackwell Scientific Publ., Boston. 220pp.

• Elseth, G. D., and K. D. Baumgardner. 1981. Population biology. D. Van Nostrand Co., New York. 623pp.

• Krebs, C. J. 1972. Ecology: The experimental analysis of distribution and abundance. Harper & Row, Publ., New York. 694pp.

• Ricklefs, R. E. 1979. Ecology, second edition. Chiron Press, New York. 966pp.

• Wilson, E. O., and W. H. Bossert. 1971. A primer of population biology. Sinauer Assoc., Inc., Sunderland, Mass. 192pp.

Revised: 02 November 2004