Fall 2004
Before discussing band recovery analysis a basic introduction to life tables will be helpful.
| Life tables are used to describe age-specific mortality and survival rates for a population. When this information is combined with fecundity data, life-tables can be used to estimate rates of population change (e.g., r, lambda, and Ro). |
Cohort or age-specific or dynamic life tables: data are collected by following a cohort throughout its life. This is rarely possible with natural populations of animals. Note: a cohort is a group of individuals all born during the same time interval.
Static or time-specific life tables: age-distribution data are collected from a cross-section of the population at one particular time or during a short segment of time, such as through mortality data. Resulting age-specific data are treated as if a cohort was followed through time (i.e., the number of animals alive in age class x must be less than alive in age class x-1). Because of variation caused by small samples, data-smoothing techniques may be required (see Caughley 1977).
Composite - data are gathered over a number of years and generations using cohort or time-specific techniques. This method allows the natural variability in rates of survival to be monitored and assessed (Begon and Mortimer 1986).
Semelparity - Individuals that have only a single, distinct period of reproductive output in their lives, prior to which they have largely ceased to grow, during which they invest little or nothing in survival to future reproductive events and after which they therefore die (Begon et al. 1996:147). For annual species, this results in nonoverlapping generations. Examples other than annual plants and some insects?
Iteroparity - Individuals that normally experience several or many such reproductive events. During each period of reproductive activity the individual continues to invest in future survival and possibly growth, and beyond each it therefore has a reasonable chance of surviving to reproduce again (Begon et al. 1996:147). Results in overlapping generations.
Birth pulse - reproductive activity is restricted to a specific breeding season. Begon et al. (1996) refer to this as "overlapping semelparity."
Birth flow - reproductive events merge into a single extended period.
| x = | age, measured in years or some other conventional unit. With longer-lived animals and plants this is often 1 year, but for voles it might be 1 week and for some insects 1 day. Often expressed as an interval, e.g., 0-1 years old. |
| nx = nx-1 - dx-1 | the number of individuals surviving at the start of age interval x. Note: n0 = sum(dx) if dx expressed as numbers dying and the survival schedule is complete for all members of the cohort. |
| dx = nx - nx+1 = | the number of individuals of a cohort dying during the age interval x to x+1. Note: sometimes calculated as proportion dying. |
| qx = dx / nx = | finite rate of mortality during the age interval x to x
+ 1. Note: this parameter is least affected by bias in the sample and gives the most direct projection of the mortality pattern in a population. It is often used to make comparisons within and between species. |
| Sx = (nx-dx)/nx or 1 - qx = | finite rate of survival during the age interval x to x + 1. This parameter is used in harvest calculations and in population modeling. Note: finite rates cannot be added to get total survival rate for a longer period of time; however, finite survival rates are multiplicative (i.e., survival from age 0 to 3 = S0 x S1 x S2). |
| lx = nx / n0 = | the proportion (scaled from 0 to 1) of individuals surviving at the start of age interval x. You will also see lx expressed per 1,000, i.e., = (nx / n0)1000 . This parameter is used to plot survivorship curves (see comments below). |
| kx = log10 nx - log10 nx+1 = | killing power or a standardized measure of the intensity (rate) of mortality. Unlike qx-values, kx-values can be added to determine the mortality rate for a number of age classes. Note: because kx-values are calculated using log10, you must take the antilog of the common log to convert back to finite survival (i.e., S = 10-k). |
| mx = | fecundity rate (i.e., average number of female offspring produced per female in the population over some period of time, generally a year). |
| lx mx = | The mean number of female offspring produced by females in an age class. This information is used to calculate net reproductive rate (R0) and the instantaneous rate of change ( r ). |
| R0 = [sum (lx mx)] / l0 = | the net reproductive rate per generation. Or in other words, the mean number of female offspring produced by a female during her lifetime (i.e., the replacement rate). Note: R0 < 1 indicates the members of the population are not replacing themselves (i.e., the population is declining). R0 > 1 denotes an increasing population. R0 = 1 indicates a stationary or "stable" population. |
| G = Sum(lx mx x) / R0 = | the mean length of a generation. Other definitions include (1) the time elapsing between birth of a female and mean time (age) of birth of her offspring and (2) the average age that adult females give birth. |
|
|
the finite rate of population change or the net reproductive rate over some time interval, which is a year in many cases. Lambda >1 indicates an increasing population, lambda=1 indicates a stationary population, and lambda<1 indicates a decreasing population. The use of this parameter is geared toward organisms that reproduce during a short breeding season (i.e., discrete growth or birth-pulse fertility). Note: your textbook uses "R" to denote lambda. |
| r ~ = ln(R0)/G = ln(lambda) = | intrinsic or instantaneous rate of increase (i.e., the change in population size per individual per unit of time). An r>0 indicates an increasing population, r=0 indicates a stationary pop'n, and an r<0 indicates a declining population. Note: the equations listed only give you an approximation of r. You need to solve Euler's equation for a precise estimate of r (see Begon et al. 1996:165). |
| ex = Tx / Lx
= where Lx = (lx + lx+1) / 2 |
mean expectation of further life for individuals alive at the start of age interval x. The mean expectation of further life can be used as one way of compressing an entire life table into one number. It has limited application for wildlife studies, but is commonly used in the insurance business. |
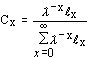 |
= stable age distribution (i.e., where the proportion of the population in each age class remains constant over time). This is only achieved if the observed survival and fecundity schedules remain constant over a long period of time. Note: population projections from simple deterministic growth models (e.g., the exponential and logistic growth models) are based on the assumption that the population has a stable age distribution. |
NOTE: Population ecologists do not all use the same life-table notation. For example, Begon et al. (1996) use different symbols to denote the finite rate of increase and mean generation length. Nevertheless, data and calculations in the respective columns have the same meaning.
Age at Death Recorded Directly - the number of individuals dying in successive intervals of time is recorded for a group of individuals born at the same time. This is the most precise type of data available because it is based on a single cohort followed through time. The observed data are the dx column of the life table.
Cohort Size Recorded Directly - The number of individuals alive in successive intervals of time is recorded for a cohort of individuals. These data are similar to those obtained with Method 1, except that those surviving are tallied, not those dying. These data are also precise and specific to the cohort studied. Observed data are entered into the nx column of the life table.
Age at Death Recorded for Several Cohorts - Individuals are marked at birth and their death recorded, as in Method 1, but several cohorts are pooled from different years or seasons. These data are usually treated as if the individuals were members of one cohort and the analysis of Method 1 is applied.
Age Structure Recorded Directly - The number of individuals aged x in a population is compared with the number of these that died before reaching age x+1. The number of deaths in that age interval, divided by the number alive at the start of the age interval, gives an estimate of qx directly.
Ages at Death Recorded with a Stable Age Distribution and Known Rate of Increase - Often it is possible to find skulls or other remains that give the age at death of an individual. These data can be tallied into a frequency distribution of deaths and thus give dx directly.
Age Distribution Recorded for a Population with a Stable Age Distribution and Known Rate of Increase - In this case, the age distribution is measured directly by sampling. The number of individuals born is calculated from fertility rates.
Note: Methods 5 and 6 are based on the critical assumption that the rate of population change is known (or the population is stationary, i.e., r=0) and the age distribution is stable. Although methods 5 and 6 appear more realistic in terms of data collection, there are numerous ways in which time-specific life tables have been calculated incorrectly, e.g., from hunter kills (see Caughley 1977).
The main value of a life table lies in what it tells us about the population's strategy for survival (i.e., life tables help us to understand the dynamics of populations). For example, time-specific life tables, although often not meeting the assumptions necessary to estimate survival rates, are valuable to a manager of exploited populations because they show the existence of strong year classes or help identify weak age classes.
Although we have used age-structured schedules, for some organisms age is not the best life history variable on which to develop analyses of population change. For example, the stage of development (egg, larval, pupal, adult stages) of some insects may be a more important life history variable. If predation on fish is size-dependent, then size rather than age would be the appropriate stage-variable.
Opportunities to follow cohorts for long periods of time are rare, which precludes cohort analysis, and the critical assumption of a stable-age distribution is so difficult to meet that it makes the use of time-specific life tables (Johnson 1994).
Survivorship curves are usually created by plotting lx on the y-axis and age on the x-axis. Occasionally you may see nx plotted on the y-axis. The y-axis is usually logarithmic, i.e., log10 (lx), to allow comparisons among different studies and species. In other words, log transformations standardize the survivorship curve.
Mortality curves are created by plotting qx or kx against age.
The band recovery models encompass the suite of models where recaptures (recoveries) of marked individuals are terminal. Therefore, marked animals are not released back into the population following recovery.
Band recovery analysis in the past has been done using composite dynamic life tables, but newer modeling approaches have been developed. These new approaches are incorporated into various software programs.
The models used in band recovery analysis attempt to estimate the following parameters.
Parameters Estimated
Annual mortality (or survival) rate varies only with age of the bird, no time-specific variation is allowed.
Annual recovery rate is constant fraction of annual mortality rate (i.e., reporting rate is assumed to be constant over all ages and years).
Virtually none of the banded birds remain alive when the data are analyzed.
There is no year-to-year variation in either harvest rates or band-reporting rates.
There is no loss of bands (note: violation of this assumption is especially serious under the C-D life table method).
Must wait until all individuals have died
Reporting rate is not a constant and often varies by age (violates assumption #2).
Often a high correlation between survival rate and reporting rate (violates assumption #2).
Band loss rates produces a negative bias in estimates of survival (violates assumption #5).
Band loss and mortality of banded birds cannot be differentiated in life-table methods (an especially serious problem when working with long-lived species).
Banding data (mostly birds) have been improperly analyzed using life-table methods. This has resulted in confusion and incorrect interpretations (Anderson et al. 1981, 1985).
Assumptions of any specific model are explicit and often appear quite general and realistic.
Goodness-of-fit tests allow the assumptions of any give model to be tested.
Choice of "best" fitting model is based on tests between models and goodness-of-fit tests.
Use of maximum likelihood estimators (MLE) results in consistent estimators that have smaller variances and, therefore, are more precise.
Annual changes in band-reporting rates do not bias the estimates of survival rates if recovery rates are allowed to be year-dependent.
Estimates of sampling variances and covariances can be computed as a measure of precision.
Can statistically test null hypotheses about the average survival in two geographic areas.
Do not have to wait until all animals have died to analyze data.
Can estimate survival/mortality with fewer assumptions than with C-D life table methods.
Analysis is based on a stochastic model structure.
Do not get age-specific survival estimates (in most cases).
Requires huge banding effort, especially for species with a low recovery rate.
Survival rates cannot be determined for the last banding year.
|
|
Note: Survival rates cannot be estimated accurately if only young are banded, regardless of the method used! |
F = recovery rate
r = band-reporting rate
Hr = harvest rate
Kr = kill rate
Mr = annual mortality rate
Program MARK: Interactive program allowing the design of particular models of interest.
Program ESTIMATE: age-independent models (i.e., banding data from adults only).
Program BROWNIE: age-dependent models (e.g., banding data for adults and juveniles)
Program SURVIV: powerful program designed for radio telemetry data but can be used to analyze banding data.
Several others...
Note: All these software programs plus others are available at the Patuxent Wildlife Research Center software web site (http://www.mbr-pwrc.usgs.gov/software.html)
XV. Program MARK
Program MARK allows you an almost unlimited number of models that you can develop to analyze your data set. This program also can handle a wide variety of data types and performs a numerous array of estimation procedures. The unlimited number of models that MARK allows you to run for a given data type is an artifact of the design matrix and parameter index matrices. These features allow you to create the various biologically relevant models that you want to test for in your data set. For this lab we will only utilize the parameter index matrices (PIM’s). MARK also uses powerful analysis methods and statistical procedures to develop and test models.
A. Models
Models can be created using the parameter index matrices (PIM’s), which are matrices used to identify individual survival and recovery rates relative to year of capture (cohort) and year of recovery. Let’s build a simple example for 4 banding occasions and 4 years of band recovery. First we will build the matrix of expected proportions (the product of survival (s) and recovery (r) probabilities) for time dependent models, then we will break this apart to develop the PIM’s. [Note: In MARK r is used for the recovery rate instead of f]. For our example the matrix of expected values is:
r1 s1r2 s1s2r3 s1s2s3r4
r2 s2r3 s2s3r4
r3 s3r4
r4
The rows indicate year of banding and the columns are the year of recovery. The first cell in the first row is the probability of recovery during the first year of recovery. The second cell is the probability of surviving the first year and being recovered the second year. As you follow these probabilities you see that recovery and survival rates depend on the year of recovery (columns), but not on the year of banding (rows). In other words s and r values vary between columns but not between rows. For example, in row 2, which is Year 2 of banding and Year 2 of recovery, the recovery rate (r2) is the same as the prior year (row 1 = Year 1 of banding). But in the next year of recovery (column 3 = Year 3 of recovery), which is still the same year for banding (Year 2), the recovery rate changes (r3).
Now we will build this in the form of PIM’s but also add in two groups representing males and females that have different survival rates. The numbers in the PIM’s identify individual parameters in a linear model. The actual value in each cell is meaningless, they are just identifiers. So we will build 4 different models using 4 recovery periods to help you understand the design of the PIM’s.
Model: Recovery and survival rates vary across time (year of recovery) and between groups (sex) or [s(g*t)r(g*t)].
Male Survival Female Survival
1 2 3 4 5 6 7 8
2 3 4 6 7 8
3 4 7 8
4 8
Male Recovery Female Recovery
9 10 11 12 13 14 15 16
10 11 12 14 15 16
11 12 15 16
12 16
The first difference and one that must be maintained for all models is that the PIM’s for survival are different than the PIM’s for recovery. Within each matrix we see that the values within each column are the same. This indicates that there is no cohort effect or that the rates for animals banded in one year are the same as those banded in other years within a given year of recovery. However, the numbers are different within each row of the PIM’s. This indicates that the rate varies with year of recovery. Interpreting the male survival PIM, we see that survival in the first year of recovery is different than survival in the second year, which is different than the third, which is different than the fourth. In other words survival rates are different from one year to the next. However, within a year survival rates are the same for each banded cohort. Now compare male survival to female survival PIM’s. We see the exact same pattern in this PIM but with different numbers. Again we have survival rates changing from year to year but no cohort differences. Then why are the numbers different between the male and female survival PIM’s? They are different because we are modeling the possibility that survival rates between males and females are different. Take the second year of recovery for example, we see that survival for all banded male cohorts is the same and survival for all banded female cohorts is the same but survival is different between males and females. Now use this same logic on the PIM’s for recovery. Keep in mind that the PIM’s for recovery can NEVER contain any of the same values that occur in the survival PIM’s. We will now present 3 more sets of PIM’s for constrained situations of the above model. Take some time and figure out what these PIM’s are modeling in regards to survival and recovery rates relative to recovery year, group (sex), and cohort or year of banding.
MODEL: Recovery and survival rates vary with year of recovery but no group (sex) differences in these rates or [s(.t)r(.t)].
Male Survival Female Survival
1 2 3 4 1 2 3 4
2 3 4 2 3 4
3 4 3 4
4 4
Male Recovery Female Recovery
5 6 7 8 5 6 7 8
6 7 8 6 7 8
7 8 7 8
8 8
Model: Recovery and survival rates are different between groups (sex) but no differences relative to time (no differences with respect to year of recovery) or [s(g.)r(g.)].
Male Survival Female Survival
1 1 1 1 2 2 2 2
1 1 1 2 2 2
1 1 2 2
1 2
Male Recovery Female Recovery
3 3 3 3 4 4 4 4
3 3 3 4 4 4
3 3 4 4
3 4
Model: Recovery and survival rates do not differ relative to group (sex) or time (year of recovery) or [s(..)r(..)].
Male Survival Female Survival
1 1 1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1
1 1
Male Recovery Female Recovery
2 2 2 2 2 2 2 2
2 2 2 2 2 2
2 2 2 2
2 2
Take the time to go through all of these models and make sure you understand them. They are crucial to understanding how the program works and how to interpret the results. Once you understand these models see what other biologically relevant models you could come up with.
A. Selecting the best model
1. Goodness-of-fit (important to evaluating an individual model but not necessarily helpful in model selection).
2. Tests between models (Likelihood ratio tests): Models must be nested.
3. Information Criteria: balancing tradeoffs between bias and variance
Akaike’s Information Criteria (AIC)
Mathematical and statistical models are very important tools for ecologists. We build models to try to answer biologically relevant questions. We use models to try to predict how a variable will act in a system or how the entire system will respond to an individual variable or a group of variables. How do you decide how many terms or variables to include in the model?
A basic concept behind building any type of model selection criteria is finding a balance between bias and variance. Bias is the difference between the expected value and the true value. Variance is the mean squared deviation of individual observations from their mean. The fewer the number of terms in the model, the lower the variance due to fewer estimations that need to be calculated. Conversely, the more terms included in the model, the smaller the bias.
AIC is a statistical calculation used to determine how many terms are appropriate for the model given the data. An AIC statistic is calculated for each model, constantly comparing it to the full model or the model containing all of the possible variables.
The model producing the lowest AIC statistic is considered to be the best choice. AIC is an objective approach where the modeler does not choose his/her favorite. Any inferences from the model are only those justified by the data.
AIC is based on the Kullback- Leibler "distance" between two models where:
AIC = - 2 ln (L) + 2 K
- ln(L) is the value of the log-likelihood function evaluated at the maximum (or the deviance from the "true model")
- K is the number of parameters in the model
The first term [- 2 ln (L)] is a measure of the lack of fit
The second term (2 K) is a "penalty" for the addition of more parameters
XVI. Assumptions of Modern Analysis Methods
|
|
Note: In practice, assumption #9 is a series of very specific assumptions that can be tested using information from the recovery array. These assumptions specify the exact model structure (i.e., Model 1, Model 2, etc.) and usually are the only testable assumptions in most banding studies. |
Generally, the survival rate is for the period between bandings, i.e., it is not the survival rate for the period between hunting seasons. Of course, this depends on when banding occurred.
The time interval between banding periods is assumed to be equal.
Studies where only a few birds are banded each year (e.g., <300) usually result in poor estimates (i.e., large variance). In addition to the total number of birds banded, recovery rate also affects sample size. For example, a species having an average recovery rate of <1% (such as blue-winged teal and American woodcock) require a very large banding effort (i.e., 2,000 to 3,000 birds per year) before survival and recovery can be estimated with any precision (and accuracy). BAND2 is a computer program for estimating sample size requirements (available at http://www.mbr-pwrc.usgs.gov/software.html).
Effects of band loss, late reporting, heterogeneous survival rates, etc.
band loss: may result in slight negative bias; significant problems only with long-lived species experiencing severe band loss.
late reporting: delayed reporting can result in a overestimates of survival; however, models in program ESTIMATE are generally robust to delayed reporting of band recoveries.
heterogeneous survival rates: if sampling is nonrandom and heterogeneity of survival and recovery rates is present, then any estimates could be misleading (e.g., tend to underestimate annual survival). If survival rates are homogeneous but recovery rates are heterogeneous, then there should be no bias in survival estimates. Note: heterogeneous rates can result from having various "subgroups" in your data set (e.g., subpopulations of Canada geese, males and females, pooling banding data from several geographic areas, etc.)
Modern analysis methods for banding data are potentially applicable to a wide range of field studies in addition to bird banding. For example, fish-tagging studies, bat banding, marking studies of herpetofauna, marine and terrestrial mammals, and a wide variety of entomological investigations.
Brownie, C., D. R. Anderson, K. P. Burnham, and D. S. Robson. 1978. Statistical inference from band recovery data - a handbook. U.S. Fish Widl. Serv. Resour. Publ. 131.
Brownie, C., D. R. Anderson, K. P. Burnham, and D. S. Robson. 1985. Statistical inference from band recovery data – a handbook. Second edition. U.S. Fish Wildl. Serv., Resour. Publ. 156, Washington, D.C. 305pp.
Revised: 06 October 2004