Use a computer model based on the Lotka-Volterra competition equations to gain a more intimate understanding of the factors that can influence the outcome of competition in a simple environment.
Use a computer model based on Tilman's resource competition model to evaluate how resource dynamics can influence the outcome of competition.
Competition among members of the same species. Intraspecific competition leads to the stable regulation of population size within limits imposed by the environment.
Theoretically, intraspecific competition may produce within-species patterns of differential resource use (i.e., habitat generalists).
Ricklefs (1979) – Competition among two or more species. Interspecific competition may cause the extinction of one of the competing populations or, at the very least, profoundly affect population dynamics and carrying capacity of the competing species.
Emlen (1973) – Interspecific competition occurs when two or more species experience a depressed growth rate or a depressed equilibrium-population level attributed to their mutual presence in an area.
Theoretically, interspecific competition leads to resource specialization and separation of species along some resource gradient (i.e., interspecific competition influences the realized niche of a species). Theoretically, each species should evolve to a form in which inter- and intraspecific competition are optimally offset (Begon and Mortimer 1986).
Birch (1957) – Competition occurs when animals utilize common resources that are in short supply, or if resources are not in short supply, competition occurs when the animals seeking that resource nevertheless harm one another in the process.
There are 3 important points associated with this definition:
The interaction between two species will be reciprocal, i.e., causing demonstrable reductions in survival, growth, or fecundity of each species. However, one species often is more negatively affected than the other.
A resource is in short supply. Even if animals overlap completely in resource utilization, competition usually does not occur unless a resource is limited in some way.
The implication of #2 is that competition is density dependent.
Interference competition – includes aggressive interactions in which one individual actively attempts to exclude another (e.g., Blue jay at a bird feeder).
Exploitation competition – indirect competition in which one species uses more of the limited resource or uses the resource more efficiently than another species. Exploitative competition can result in depletion of a resource by a species or it may involve some activity that makes the resource virtually valueless to another species.
Other ways to classify or categorize competition: passive, active, scramble, contest.
Lotka-Volterra model is based on logistic model of population growth:
dN/dt = rm N (1 - N/K)
The logistic-model of population growth includes a density-dependent component (within the parentheses) that reflects the impact of intraspecific competition on survival and reproduction.
The Lotka-Volterra model incorporates interspecific competition by using a parameter called alpha. Alpha is the coefficient of competition (or competition coefficient) and measures the competitive effect of one species on another. For example:
a12 is the effect of species 1 on species 2.
a21 is the effect of species 2 on species 1.
Note: the notation for competition coefficients is not consistent among textbooks or computer programs (output). For example, Begon and Mortimer (1986) define a12 as the effect of species 2 on species 1, which is opposite of the definition stated above. Some computer programs may use Greek symbols such alpha and beta to represent a12 and a21, respectively. The bottom line is to make sure you understand the notation used by a particular author or computer model.
Regardless of the notation used, the coefficient of competition measures interspecific competition relative to intraspecific competition, e.g., how many individuals of species 2 are equivalent to one individual of species 1 in terms of their use of the resource. For example:
If one elk (species 1) is equivalent to 3 deer (species 2) in terms of its use of the resource and its effect on species 2, then a12 = 3.0. If the effect of species 2 on species 1 is reciprocal (i.e., if 1 deer is equivalent to 0.33 elk), then a21 = 0.33. Note: the alpha's of each species do not have to be reciprocal.
An alpha > 0 indicates that there is some overlap in resource utilization. In the real world, alpha is probably between 0 and 1 for species with similar niches, which indicates there is probably some partitioning of resources. Why? Hint: how does this relate to the Competitive Exclusion Principle?
Remember the logistic growth model:
Population growth of species 1 in the presence of species 2:
Population growth of species 2 in the presence of species 1:
| The zero-growth isocline describes expected equilibrium population sizes of one species if abundance of the second species is held constant, and vice versa. The relationship between the two species is assumed to be linear, i.e., the isoclines for species 1 and species 2 can be written as equations for a straight line (y = a + bx). |
1. Plot N2 on the y-axis and N1 on the x=axis (to be consistent with output from the simulation program that you will use in lab today).
2. Determine the zero-growth isocline for species 1:
Set dN1/dt = 0
Rearrange the Lotka-Volterra equation for species 1 (solving for y = N2):
or
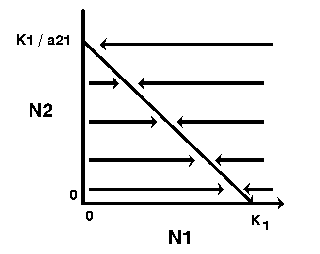
Thus, the zero-growth isocline for species 1 is a straight line (y = a + bx) with the y intercept = K1/a21 and slope (b) = 1/a21 (assuming N2 is plotted on the y-axis).
The zero-growth isocline for species 1, at constant levels of species 2, can be visualized with a phase-plane diagram:
3. Determine the zero-growth isocline for species 2:
Set dN2/dt = 0
Rearrange the Lotka-Volterra equation for species 2 (solving for y = N2):
Thus, the zero-growth isocline for species 2 is a straight line (y = a + bx) with the y intercept = K2 and slope (b) = a12 (assuming N2 is plotted on the y-axis). Note: the x intercept is derived by solving the above equation for N1 when N2 = 0 (i.e., x intercept = K2 / a12).
The zero-growth isocline for species 2, at constant levels of species 1, can be visualized as follows:
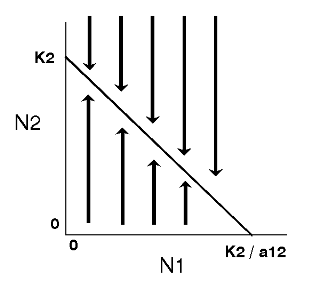
| Thus, the growth of species 1 will be zero when N2 = 0 and N1 = K1 , or when N1 is close to zero and N2 = K1/a21. Likewise, the growth of species 2 will be zero when N1=0 and N2 = K2 , or when N2 is close to zero and N1 = K2/a12 . |
The expected outcome of competition can be examined by superimposing the phase-plane diagrams for each species (i.e., plot the zero-growth isoclines) and using vector addition (the arrows) to depict changes in population size of each species.
Note: There are 4 possible outcomes in the Lotka-Volterra model of competition based on the 4 ways that the zero-growth isoclines can be arranged:
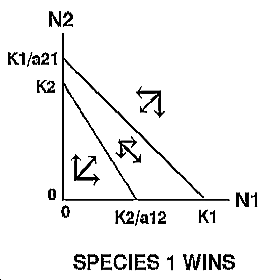
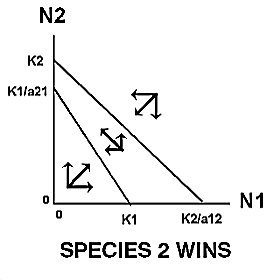
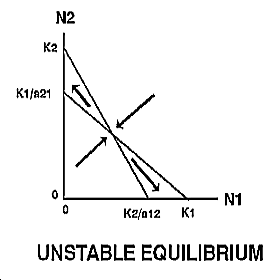
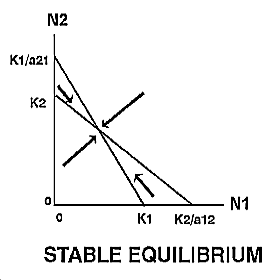
The outcome of competition, according to the Lotka-Volterra model, is ultimately determined by carrying capacity (Ki) and the competition coefficient (aij) of the two species. We will use program POPEC to explore the logistic-competition theory. |
|
Assumptions of the Lotka-Volterra logistic-competition model:
|
Logistic-competition theory is based on the dynamics of the consumer populations involved, i.e., it does not explicitly consider changes in resources utilized by the competitors. As discussed in lecture, Tilman (1982) treated the regulation of population size from the standpoint of resource dynamics, i.e., supply and consumption.
A resource is defined as any substance that is consumed by an organism and which leads to an increased per capita growth rate as its availability is increased. If a species is consuming a single limiting resource, the population may eventually reach an equilibrium in which b = d, and the rate of supply of the resource equals its consumption rate.
According to Tilman's model(s), the outcome of competition depends on:
The relative position of the Zero Net Growth Isoclines (ZNGI),
the resource consumption rates of each species, and
the relative supplies of each resource in the absence of consumption (the resource supply points).
We will use program POPULUS to explore Tilman's resource-competition model. Note: we will use the "competition for essential resources" option to model competition for 2 limiting resource.
There are many different ways that a species can respond to 2 resources. One possible response is that of plants to nitrogen and light. These resources are essential. For perfectly essential resources, the growth rate of a plant is determined by the one resource in lowest supply compared to its need. Thus, the growth rate of a plant is determined by the concetration of the one resource that leads to the lowest growth rate.
Two species can coexist when consuming 2 essential resources if each is limited by a different resource and each, relative to the other species, consumes more of the resource which limits it.
Notation for the resource-competition model:
Ni = population density.
Ri0 = concentration or availability of the limiting resource.
Ri* = concentration of the resource required for growth of the species to equal its loss rate.
ri = maximal per capita growth rate of the consumer species.
ki = resource concentration at which the species attains half its maximal growth rate.
mi = mortality rate or loss rate the consumer experiences.
Si = supply point for a habitat, i.e., the maximal amount of the resource in the habitat.
ai = the rate at which the resource is converted from an unavailable to an available form.
ci = the resource consumption rate of the consumer species.
Note: setting Ri0 = Si means that all of resource i in the habitat is available for use.
| Note: Both Tilman's and Lotka-Volterra's model of competition lead to a similar conclusion: coexistence is made possible by ecological segregation, at least in theory! |
Tilman, D. 1980. Resources: a graphical-mechanistic approach to competition and predation. American Naturalist 116:362-393.
Tilman, D. 1982. Resource competition and community structure. Princeton University Press, Princeton, New Jersey. 296pp.
Revised: 28 November 2011