Up until now, in this section of population growth, I have discussed growth in an unlimited environment. This phenomenon is essentially described using an exponential function. In the equation Nt = N0ert the calculation of r assumes the environment is not limiting. But what if some part of the environment is limiting? As we know, populations in actuality do not increase forever, because something or a combination of things (limiting factors) hold down population growth.
Birch did a very interesting experiment with weevils (Calandra oryzae). He introduced a female and a male weevil into 12 grams of wheat at a constant temperature and humidity, and followed the change in number of adults for 100 weeks (almost 2 years). There were, of course, fluctuations in the food supply as it was eaten, but the food supply was more or less constant.
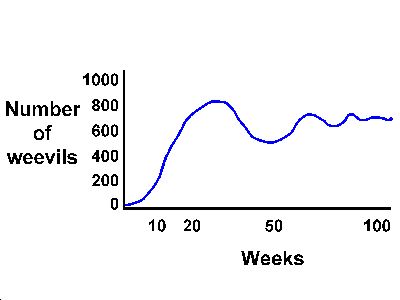
Features of the experiment:
At the beginning, the growth of the population is almost exponential, increasing close to the intrinsic rate of increase.
After the tenth week, the rate of increase begins to slow, and at about the twentieth week the population plateaus.
After that, the population fluctuates around a mean of about 700.
Other experiments of this nature have shown similar results.
I previously pointed out that the intrinsic rate of increase is equal to r, which equals the intrinsic birth rate (b) minus the intrinsic death rate (d). In an unlimited, constant environment, the birth rate and death rate do not change, and consequently neither does r. But observations such as Birch’s experiment indicate that the rate of population growth progressively slows as the number of individuals reaches maximum possible density. Somehow, the increase in density causes the birth rate to decrease, the death rate to increase, or both. At the plateau, b equals d and therefore r equals 0.
The initial growth of a population up to the plateau is roughly an S-shaped curve. The earliest attempt to simulate this curve was the logistic equation of Verhulst (1839). The S-shaped or logistic curve differs from the geometric curve in two ways:
It has an upper asymptote (the curve does not exceed a certain maximum level), and
it approaches this asymptote smoothly, but abruptly. In fact, when you divide the curve at its inflection point, the upper and lower halves are mirror images of each other.
The reasoning behind the logistic curve is simple. The population density increases but at higher densities, the rate of increase decreases. At some maximum density, it does not increase at all.
The logistic growth equation has proven remarkably useful in population ecology. The equation seems to describe growth reasonably well for a number of populations. Yeast and protozoan growth curves, for example, fit the model quite well, as to a less precise degree do those of same metazoans. Gause found reasonable fits for Paramecium and for flour beetles (Tribolium), and Pearl found the logistic equation to fit quite accurately the growth in Drosophila melanogaster populations.
While growth curves similar to those predicted by the logistic growth model are occasionally found, most metazoans do not show very good fits to the equation. In fact, growing metazoan populations usually show quite regular damped oscillations. These oscillations appeared under quite constant laboratory conditions, and therefore were not due to environmentally induced fluctuations in r. The question is, why should the oscillations occur?
As Krebs point out, the simplest way to produce an S-shaped curve is to introduce into our geometric equation (the integral of dN/dt, Nt = N0ert) a term that will reduce the rate of increase as the population builds. We also want to reduce the rate of increase in a smooth manner, and this is accomplished by making each individual added to the population reduce the rate of increase an equal amount. The classic way of describing the progressively increasing environmental resistance to further growth is shown by the addition of the “dampening factor” (X - N) / K to the above differential equation.
Thus, dN/dt = rN [(K-N)/K]
r = growth rate constant
K = the maximum number of individuals that the given environment can support, i.e. the upper limit of population growth
Basically, this equation states that:
Rate of increase of population per unit of time (dN/dt) = Innate capacity for increase (rmax) x Population size (N) x Unutilized opportunity for growth (K-N / K).
Integration gives an algebraic form of the so-called logistic equation:
Nt = K / (1 + A e-rt), where A = constant
This equation can be written another way by rearranging the terms:
ln [(K-N) / N] = a - rt
This is also the equation of a straight line in which the coordinates are:
Y coordinate = ln (K-N / N)
X coordinate = time
Two attributes of the logistic curve make it attractive:
mathematical simplicity, and
- apparent reality.
The biological meaning of K is essentially the density at which the space being studied becomes “saturated” with organisms (the carrying capacity).
The population has an initially stable age distribution
The density has been measured in appropriate units.
There is a real attribute of the population corresponding to r, the intrinsic rate of increase.
*The relationship between density and the rate of increase is linear – probably violated in many growing populations.
* The depressive influence of density on the rate of increase operates instantaneously, without any time lapse. Highly unlikely that in organisms with complex life cycles the rate of population increase could respond instantaneously.
At one time, it was suggested that the logistic curve per se described a fundamental law of population growth. This viewpoint has largely been abandoned over the years as early predictions about human population growth (rates and upper limits) proved grossly incorrect and more field data on growth in other species became available.
 |
The real value of logistic theory is that it introduces us to such concepts as density-dependence and mean population level. |
Return to Lecture Notes IX: Population
Growth - Limited Environments. 
Updated 06 August 1996
