Figures Inscribed in Curves
A short tour of an old problem
by
Mark J. Nielsen
Professor of Mathematics
University of Idaho
These pages give a brief and informal
introduction to one of my favorite unsolved
mathematics problems -- the so-called "inscribed squares problem".
The question can be informally stated as follows:
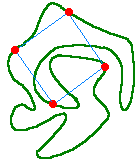
If you draw a curve on a piece of
paper that ends where it began but never
crosses itself (such as the green curve at right), will it always pass through
the four corners of some square?
Notice that we don't care whether or not the square "stays inside" of
the curve -- in fact, its sides may cross the curve many times.
Nor do we care whether or not the corners of the square appear on the
curve in any particular order.
A more exact statement of the question requires a couple of (fairly simple)
definitions.
- A simple closed curve is the image in the
plane R2
of a continuous function f: [0,1] ----> R2
that is one-to-one except that f(0) = f(1).
Intuitively, this is exactly what you'd expect a "closed curve" to be --
you start drawing at some point and trace a curve without lifting your
pencil from the paper and without making your curve cross itself, ending
at the point where you began. The word "simple" refers to the fact that the
curve doesn't cross itself.
- Let J be a simple closed curve.
We'll say that a polygon P is inscribed in J if its
vertices lie on J.
The inscribed squares problem can now be stated efficiently as:
Does every simple closed curve have an inscribed square?
To me, this is an appealing problem for several reasons:
- It is easy to state and understand the question.
- It has a nice geometric flavor (with a touch of topology for interest).
- It has avoided a complete solution for a long time.
The problem was first posed by Toeplitz in 1911, and
while many interesting partial and related results have been given,
no one knows the answer to the question above. In fact, the "range of
ignorance" with regard to this question is quite astounding!
For all the work that has been done on this question, we don't yet
know enough to rule out either of the
following extreme possibilities:
Possibility One: Every closed and bounded set that separates the
plane into more than one piece must contain the four vertices of a square.
Possibility Two: "Most" simple closed curves do not have inscribed
squares. (By this we mean that if you were to draw a simple closed
curve at random from the set of all simple closed curves, the probability
that you'd get one with an inscribed square is zero. This notion can be
made exact in several different ways, all of which involve details that we
don't want to get into here!)
Given that we can't rule out either of these extremes, how much
is known? Some of the first efforts to answer the question
resulted in proofs that
all polygons, differentiable curves, and curves bounding convex regions
had inscribed squares. The best result to date is probably the
following theorem (1989) due to Walter Stromquist.
Stromquist's Theorem:
If the simple closed curve J is "nice enough" then it has an
inscribed square.
[Walter Stromquist,
Inscribed squares and square-like quadrilaterals in closed curves,
Mathematika 36: 187-197 (1989).]
Here, "nice enough" means the following: for each point P
on the curve there must be a coordinate system for the plane in which some
piece of the curve containing P is the graph y = f(x)
of a continuous function.
At least one prominant mathematician
I have met believes that Stromquist's theorem is good enough to make the
statement "All simple closed curves have inscribed squares" morally
true -- presumably because any curve you could actually draw with pencil and
paper is nice enough to be covered by Stromquist's theorem.
In other words, this theorem more-or-less settles the informal version of
our original question -- any curve you draw on a sheet of paper
will have an inscribed square.
But the more formal version of the question is far from settled,
because "most" simple closed curves
have fractal-like behavior and are
not "nice" at all.
And while it is certainly good to have an answer for the pencil-and-paper
version, the topologist in me cares about those curves that exist only in our
imaginations. The universe of mathematics is much larger than just what
we can draw on paper -- if there are curves
that don't admit inscribed squares, I want to know about them.
Note: The following strategy
may have occured to you
as a possible way to get an inscribed square in an arbitrary
(probably not-very-nice) curve J:
- Approximate J by a
sequence of "nice" curves (such as polygons) P1,
P2, P3, . . .
- Use Stromquist's Theorem to get a square Qi
inscribed in each Pi.
- Take a limit of the squares Q1,
Q2, Q3, . . . (or more properly of
some subsequence of this sequence of squares) to get a square inscribed
in J.
This actually works perfectly well with one small but crucial catch: we
can't guarantee that the sizes of the squares Q1,
Q2, Q3, . . .
don't go to zero in the limit. If that happens then the limiting figure
is a degenerate square -- in other words a single point! (And
proving that every simple closed curve contains an inscribed point
is not very interesting!) Because of this, any theorem that guarantees
an inscribed figure of some minimal size would be extremely
important. If we could improve Stromquist's Theorem to say that "nice"
curves have "big" inscribed squares, we'd have the whole matter settled.
But even if we are never able to ultimately answer the big question (which, by
the way, I believe we will be able to do!), investigating
the inscribed squares problem
has led to many interesting side results.
Below you will find links to six of these.
I have chosen them for the simplicity and/or
appeal of their proofs, which you can read by clicking on the
theorem name. I have stated the theorems and
proofs in their simplest, most intuitive versions, leaving off the
messy details that are often necessary to
state and prove a theorem in its most general form. If you want all the
details, the reference to the relevant research paper is provided.
The first theorem shows that the "nice" behavior demanded by Stromquist's
Theorem can be replaced by symmetry -- a different type of "nice" behavior.
You will notice in the proof that the symmetry property
reduces the number of points to be located on the curve from four
to two.
- THEOREM A:
Every simple closed curve that is symmetric about the origin has an
inscribed square.
[Mark J. Nielsen and S.E. Wright,
Rectangles inscribed in symmetric continua,
Geometriae Dedicata 56: 285-297 (1995).]
The next two theorems don't require any special behavior on the part of the
curve, but also don't quite guarantee inscribed squares. Instead, they say
we can always find inscribed four-sided figures that are related
to squares.
- THEOREM B:
Every simple closed curve has lots of inscribed parallelograms and
lots of inscribed rhombuses.
[Mark J. Nielsen, Rhombi inscribed in simple closed curves,
Geometriae Dedicata 54: 245-254 (1995).]
- THEOREM C:
Every simple closed curve has at least one inscribed rectangle.
[Proof due to Vaughan, included in the paper
Balancing acts,
Topology Proc. 6: 59-75 (1981) by Mark D. Meyerson.]
Finally, many interesting results can be proved about triangles
inscribed in curves. This is, of course, a bit easier to deal
with than squares, since the number of points to grapple with is only
three.
- THEOREM D:
If J is any simple closed curve and T is any triangle
then J has an inscribed triangle similar to T.
[Mark D. Meyerson,
Equilateral triangles and continuous curves,
Fund. Math. 110: 1-9 (1980).]
- THEOREM E:
Extending Theorem D, J has so many inscribed triangles similar to
T that the vertices of all these inscribed triangles are
"dense" in the curve J.
[Mark J. Nielsen, Triangles inscribed in simple closed curves,
Geometriae Dedicata 43: 291-297 (1992).]
- THEOREM F:
If T is any triangle and if
J is a simple closed curve in 3-dimensional
space R3 (instead
of in the plane) that is differentiable (has a tangent line) at at least
one point, then J has an inscribed triangle similar to T.
[Eric Rawdon and Jonathan Simon, unpublished(?) -- correspondence
with Professor Victor Klee.]
If you like geometry, you may enjoy reading a few of the proofs of the
above theorems (just follow the links).
For a more thorough introduction to the
inscribed squares problem, as well as many more
references to related papers, consult pp.58-65 and 137-144
in the excellent book Old and New Unsolved Problems in Plane Geometry
and Number Theory (1991, Mathematical Association of America) by
Victor Klee and Stan Wagon.
You may even feel inspired to try your own hand
at chipping away toward a solution to the inscribed squares problem.
Below you will find a few exercises to get you warmed-up,
followed by some open-ended (and as-yet-unanswered) questions.
Good luck -- as they
say in TV's The X-files, "the truth is out there somewhere."
Exercises
- Looking for examples is always a good way to warm up to a mathematics
problem!
(a) Find an example of a simple closed curve that has exactly one
inscribed square.
(b) The circle is an example of an inscribed square in which every
point is a vertex in an inscribed square. Find another such simple closed
curve.
- From Theorems D and E we know that every simple closed curve has an
inscribed equilateral triangle (lots of them, in fact!) and the whole point
of the inscribed squares problem is to figure out if every simple closed curve
has an inscribed square. Show (by giving a negative example) that not all
simple closed curves have inscribed regular pentagons.
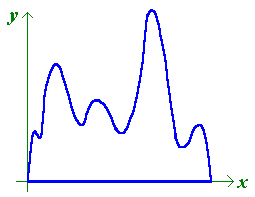
- Suppose we form
a simple closed curve by adjoining the segment of the x-axis
from x=0 to x=1 to the graph of a continuous function
f: [0,1] ---> R
such that f(0) = f(1) = 0 and f(x) > 0 for
0 < x < 1. (See the figure at right.) You don't need Stromquist's
Theorem to show that this curve has an inscribed square -- all you need is
the Intermediate Value Theorem and Extreme Value Theorem from calculus.
The proof makes a nice application of these facts -- try it!
- Use the "mountain climbing" technique (as in the proof of Theorem B)
to prove the following relative of Theorem A:
THEOREM:
Every simple closed curve
that is symmetric across some line has an inscribed square.
Open Questions
- Can you extend Theorem E say "given any simple closed curve J
and any triangle T there are at most two points of J that
are not a vertex in some inscribed triangle similar to T"? (This is
true in the case that T is an equilateral triangle -- see the note
at the end of Theorem E's proof.)
- Can you prove (or disprove) a theorem similar to Theorem E for curves in
Rn?
- Can you find a way to do away with the requirement in Theorem F that the
curve have a tangent line at one point? (This seems like an artificial
hypothesis, but is needed to make the current proof work.)
Comments or Questions about this page
can be directed to me at
markn@uidaho.edu.
Visit my
homepage.

