|
Measuring density without plots
Is a Quadrat Needed?
Counting the number of plants in a quadrat can be very time
consuming. Therefore, alternative methods have been developed that are
based on the distance between plants or the distance from a specific point and a
plant.
One unavoidable truth when measuring vegetation density is that plant
Density and Distance between Plants is inextricably linked:
High Density = Plants that are Close Together
or
Low Plant Density =Plants that are Far
Apart
Techniques based on this premise are called plotless
or distance-based techniques.
The basic idea of these distance techniques is that density can be
calculated if the average space occupied by individual plants can be
determined. These techniques assume:
Distance techniques were generally developed in forests, but they can be applied
to grasslands and shrublands if:
-
Individual plants can be easily recognized (i.e., shrubland or bunchgrass
communities)
-
Space between plants is a measurable amount (i.e., relatively sparse comm.)
Plotless techniques can have several advantages over quadrat-based techniques:
-
Usually faster (especially in sparse communities).
-
Requires less equipment - just need a way to measure distance (e.g., meter stick,
tape measure, or laser range finder).
-
Does not require selection or adjustment in quadrat size.
Basic Distance Relationships
It is not surprising that the distances between plants or between a
selected point and plants in the area are related by basic principles of
geometry. Therefore, all distance based techniques are related by this
general equation:
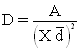
D= Density
A = Area of interest (like meter squared)
d
= Distance measured in the field
The term "X" in these
equations varies depending on assumptions about distance between plants or
points to a plant. Each technique or method includes some twist on the value for
X.
Three Basic Plotless or Distance Methods
About 8 to 10
methods have been developed to estimate and calculate density based on
distances. However, we will outline just 3 methods here following Elzinga et
al. 1998 (pages 172-173). In the examples below, focus on what is
measured and become familiar with the equation of how distance is related to
density. 1)
Point-Centered Quarter
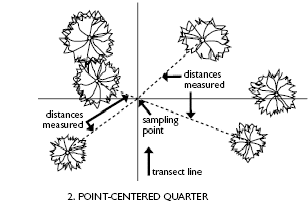
The distance from a
sample point to the nearest plant in each of four quarters or quadrants.
 Choose a
series of points in the sample area (at least 15).
Place a
“cross” or “plus” shaped guide/frame over the point.
Measure
the distance from the point to the nearest plant of interest in each of the
quadrants outlined by the cross-shaped guide.
Estimate Density:
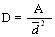
For example:
Distance of point to shrub
Quarter 1= 0.5 meters
Quarter 2 = 0.35 meters
Quarter 3 = 0.4 meter
Quarter 4 = 1.2 meters
The average distance to a plant (d)
= .61 meters
If we want to express density in number of plants/m2 then
1 m2/(.61)2 = 2.7 plants/m2
If you want to express density in number of plants per hectare in this examplethen:
There are 10,000 m2 in a ha so 10,000 m2/(.61)2
= 27,027 plants/ha
The technique
assumes that the area around plants is roughly circular and points are far enough
apart so that no plant is measured twice.
2) Nearest Neighbor
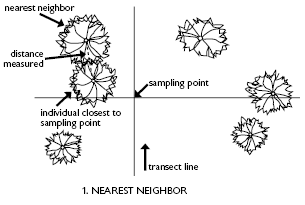
The distance from a selected plant to its nearest plant (neighbor) is measured.
Choose a
referent plant - (usually the closest individual to a selected point.)
Identify the plant closest to the referent plant and measure the distance
between these two plants.
Estimate
density:
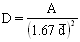
3)
Closest Individual
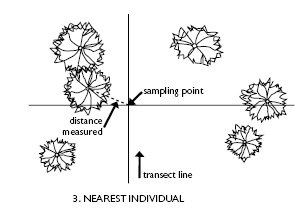
The distance from a
sample point to the closest individual is measured.
Choose a
series of points in the sample area
Measure
the distance to the closest plant of interest
Estimate density:
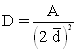
Reference
Elzinga, C.L., D.W. Salzer and J.W. Willoughby. 1998.
Measuring and Monitoring Plant Populations. Technical Reference 1730-1.
Bureau of Land Management. Denver, Colorado. USDI, BLM |
