WLF 448: Fish & Wildlife Population Ecology 2008

Lab 5: CAPTURE-RECAPTURE

I. INTRODUCTION

A. Why use capture methods?

B. Open versus closed populations

1. Closed population – a population in which there is no recruitment (birth or immigration) or losses (death or emigration) during the period of study.

   a. Geographic:

   b. Demographic:

2. Open population – a population that changes in size and composition from births, deaths, and movements.

C. Overview of capture-recapture models:

1. Closed-population models

   a. two samples – Lincoln-Petersen model (and Chapman modification)

   b. several samples (k>2) – Schnabel (Schumacher-Eschmeyer) model and models in program CAPTURE.

2. Open-population models (note: geographic closure is still a critical assumption)

   a. Cormack-Jolly-Seber models (based on k>2) in Program MARK.

3. Combination of open and closed models (Pollock's Robust Design) in Program MARK.

II. LINCOLN-PETERSEN MODEL (2-sample closed-population model)

A. Basic underlying concept of capture-recapture:

A sample of C₁ animals is Caught, marked, and released (M₂). Later a sample of C₂ animals is Captured, of which R₂ animals are Recaptures that were previously marked. If capture probability (p) is independent of marking status, then the proportion of marked animals in the second sample should be equivalent to the proportion of marked animals in the total population so that

R/C = M/N

where N is the total catchable population size. Solving for N yields the estimator:

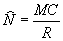
If sample size is small, the above estimator is biased. For example, what happens if the number of recaptures is zero? A modified version with less bias was originally developed by Chapman (1951) and is commonly called the modified Petersen estimate in fisheries:

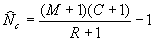
Note that Ricker (1975) and many other texts simply drop the -1 as negligible.  Chapman showed that the variance of N^{^} can be estimated as:

var (N_c^{^} ) = [(M+1) (C+1) (M- R) (C-R)] / [(R+1)² (R+2)]

An approximate 95% CI (normality for N^{^}_c is assumed) can be estimated as

N_c^{^} ± 1.965 * [var (N_c^{^} )]^0.5

B. Fundamental Assumptions of Lincoln-Petersen estimator:

1. The population is closed (geographically and demographically).

2. All animals are equally likely to be captured in each sample.

3. Capture and marking do not affect catchability.

4. Each sample is random.

5. Marks are not lost between sampling occasions.

6. All marks are recorded correctly and reported on recovery in the second sample.

Note: capture probability ( p) is often defined as the probability of an animal being caught in any trap. Possible sources of variation in p include: (1) heterogeneity (e.g., sex, age, social status, size of fish), (2) behavior (e.g., trap happy or trap shy), and (3) time (e.g., effects of weather or sampling effort on p).

III. SCHNABEL ESTIMATOR (k-sample closed-pop'n model)

A. Schnabel 1938, Schumacher and Eschmeyer 1943

This method extends the Lincoln-Peterson method to a series of samples in which there are 2, 3, 4,..., n samples. Individuals caught at each sample are first examined for marks, then marked and released. Only a single type of mark need be used because we just need to distinguish 2 types of individuals: marked, caught in one or more prior samples; and unmarked, never caught before. For each sample t, the following is determined:

C_t = Total number of individuals caught in sample t

R_t = Number of individuals already marked (Recaptures) when caught in sample t

M_t = Number of marked animals in the pop'n just before the tth sample is taken.

Schnabel treated the multiple samples as a series of Lincoln-Peterson (L-P) samples and obtained a population estimate as a weighted average of the L-P estimates which is an approximation to the maximum likelihood estimate of N:

N^ = SUM (M_t C_t) / ((SUM R_t) + 1)

Note: Var (N^ ) is a function of recaptures, therefore precision of the estimate is increased by increasing total recaptures (SUM Rt).  It can be calculated by  inverting the following: Var^(1/N) = SUM (Rt) / ( SUM (Mt Ct))^2

B. Assumptions of the Schnabel method

• Same as Lincoln-Petersen estimator but assumptions apply to all sampling periods. In other words, every individual in the population is assumed to have the same capture probability for a given sampling occasion (although capture probabilities can vary among sampling periods).

C. Advantage of k-sample methods

• The major advantage of multiple sampling is that it is possible to evaluate the data for violations of assumptions, such as unequal capture probabilities.

D. Why use a closed-population model?

IV. Program CAPTURE (for sampling closed populations)

A. Overview of models in CAPTURE

Violations of the assumptions of equal capture probabilities in capture-recapture studies can lead to unreliable estimates of population size. Program CAPTURE was developed to deal with unequal capture probabilities. It uses different estimators (models) to account for different sources of variation in capture probabilities:

M₀ = Equal Catchability Model (null model) -- Assumes every animal in the population has the same p^{^} for each sampling period in the study.

M_h = The Heterogeneity Model -- Assumes that each animal has a unique p^{^} that remains constant over all trapping occasions. Furthermore, capture probabilities are assumed to be a random sample of all individuals in the population.

M_b = The Trap Response Model -- Adjusts for a change in capture probabilities caused by a response to trapping. An assumption of the M_b model is that the initial p^{^} for all animals is the same (equal catchability).

M_bh = The Heterogeneity and Trap Response Model-- Based on the assumption that each animal has its own unique pair of potential capture probabilities, p_j and c_j (j = 1, ..., N animals in the population), where p_j is the initial capture probability and c_j is the recapture probability.

M_t = The Time Variation (Schnabel) Model -- Based on the assumption that every individual in the population has the same p^{^} for a given sampling occasion, but capture probabilities can vary at each sampling time.

Other Time-Dependent Models: M_th, M_tb, and M_tbh (Note: there was no estimator available for M_tbh until recently and it is only calculated within MARK).

B. Choosing the "best" model for your data

• Tests between models

• Goodness-of-fit tests

• Mathematical model selection procedure (i.e., Selection Criteria)

Note: The goodness-of-fit test for Model Mt has low power (i.e., even when the model is false, the test does not have a large probability of rejecting the model), especially for small populations. When Model Mb is true, there will be time variation in capture probabilities, and there will be a type of heterogeneity of capture probabilities after day 1. This will cause difficulty in selecting the appropriate model. The model-selection procedure based on tests of the assumptions (related to capture probabilities) produces eight selection criteria, one for each model. At least one criterion will be equal to 1, thereby indicating the appropriate model for the data. If the selected model has no estimator (mathematical equation), then there is apparently no valid estimator for those data. Select the most appropriate remaining model that has an estimator and use it to estimate N. Note: the resulting estimate is likely to be biased. The N^ estimate for Model Mh (the jacknife estimator) is the most robust, followed by N^bh, N^b, N^t, and N^o. Note: N^t always can be used instead of N^o.

C. Testing the "demographic closure" assumption

• Program CAPTURE includes a test for demographic closure. However, this is a weak test because a failure of closure cannot be distinguished from behavioral changes in capture probabilities or from certain patterns of time-trends in capture probabilities. In other words, the test may lead you to reject the null hypothesis of closure when in fact the population was "closed." Thus, the test is only valid if M_h or M_o is selected as the most appropriate model.

D. Using program 2CAPTURE and CAPTURE (an overview)

• Program CAPTURE now consists of 2 executable components: an analytical component (still named CAPTURE) that performs abundance and density estimation from information provided by the user, and a new (1991) component named 2CAPTURE, which provides a user-friendly interface to CAPTURE.

Note: Program 2CAPTURE is used to build the input file, which then must be submitted to program CAPTURE for analysis. You will likely run into "memory" problems if you try to run program CAPTURE from within 2CAPTURE. Instead, use 2CAPTURE to create your input file, then exit 2CAPTURE and run CAPTURE in stand-alone mode. We will show you how to do this in lab!

• Naming convention for files:

*.CAP = input file (an ASCII file containing raw data, without command lines) - used by 2CAPTURE to build an *.INP file.

*.INP = input file (an ASCII file containing command lines and, possibly, raw data) - created by using 2CAPTURE or some type of editor. This file tells CAPTURE what to do with the data. Note: older versions of program CAPTURE expect this file to be named CAPTIN.

*.OUT = output file (summary and results of analyses) from CAPTURE. If you do not designate an output file, the program will name the output files CAPTUR1, CAPTUR2, etc. If there is a run-time error, you may also end up with a FORT1 in your directory (results of analyses that were successfully executed). Note: program CAPTURE will automatically save output to a file named CAPTLP if you don't specify an output file.

• Input files (*.INP or CAPTIN) must be in the following format:

TITLE=' a title of your choice ' 
TASK READ CAPTURES (MATRIX) OCCASIONS=(#) SUMMARY FILE=optional 
DATA='a name of your choice that describes the data, source, etc.' Note:optional 
FORMAT='(Fortran code)' Note: describes data location by column number.
READ INPUT DATA 
     Data are entered here or stored in the file referenced above. 
TASK MODEL SELECTION OCCASIONS=#-# (occasions command is optional) 
TASK CLOSURE TEST OCCASIONS=#-# (occasions command is optional) 
TASK POPULATION ESTIMATE APPROPRIATE 

• Output (we will go over examples in class)

1. List of task statements, commands, warning messages, etc. Note: ignore warnings if you got a "Capture Normal End" statement on your screen.

2. Definitions of symbols/variables used in the output (you may not get this page in your output - see next section)

3. Summary of capture history for each animal (if applicable and if SUMMARY is included in the TASK READ CAPTURES line).

4. Results of model-selection tests (7 tests possible). Note: see Selection Criteria

5. Population estimates and confidence intervals

6. Test for closure (if requested and if applicable to the model selected)

• Notation used in output from program CAPTURE

t - number of trapping occasions.

n(j) - number of animals captured in the jth sample, j=1,...,t. This is the total number of captures in the experiment.

u(j) - number of new (unmarked) animals captured in the jth sample, j=1,...,t.

f(j) - the capture frequencies. The number of individuals captured exactly j times in t days of trapping j=1,...,t.

M(j) - the number of marked animals in the population at time of the jth sample, j=2,...,t. Note that M(1) equals zero.

M(t+1) - the number of distinct individuals caught during the experiment.

N^{^} - the estimated population.

p^ - estimated probability of capture.

p^(j) - the estimated probability of capture by occasion.

p-bar - average probability of capture for the generalized removal model.

c^ - estimated probability of recapture.

V. IN-CLASS EXERCISE

VI. PROBLEM SET

VII. SELECTED REFERENCES

• Krebs, C. J. 1989. Ecological methodology. Harper and Row, Publ., New York. 654pp.

• Lancia, R. A., J. D. Nichols, and K. H. Pollock. 1994. Estimating the number of animals in wildlife populations. Pages 215-253 in T. A. Bookhout, ed. Research and management techniques for wildlife and habitats. Fifth ed. The Wildlife Society, Bethesda, Md.

• Otis, D. L., K. P. Burnham, G. C. White, and D. R. Anderson. 1978. Statistical inference from capture data on closed animal populations. Wildl. Monogr. 62. 135pp.

• Pollock, K. H., J. D. Nichols, C. Brownie, and J. E. Hines. 1990. Statistical inference for capture-recapture experiments. Wildl. Monogr. 107. 97pp.

• Rexstad, E., and K. Burnham. 1991. User's guide for interactive program CAPTURE. Colorado Coop. Fish and Wildl. Res. Unit, Colorado State University, Fort Collins. 29pp. Note: TA has a copy of this manual if you have a question about program 2CAPTURE.

• Ricker, W. E. 1975.  Computation and Interpretation of Biological Statistics of Fish Populations.  Department of the Environment, Fisheries and Marine Service, Ottawa.

• White, G. C., D. R. Anderson, K. P. Burnham, and D. L. Otis. 1982. Capture-recapture and removal methods for sampling closed populations. Los Alamos Nat. Lab., Los Alamos, New Mexico. 235pp. Note: there is a copy of this manual on reserve at the UI library.

Revised: August 25, 2011