| On-target home ==> Math modeling ==> Sizing a Parachute |
SIZING A PARACHUTE
by Levi Westra
Goal
Determine the size of a parachute needed to deliver a specified payload at a specified speed
Basic Concepts
When released from rest, a parachute will accelerate before reaching a steady speed. This steady speed is called terminal velocity. Terminal velocity is a consequence of equilibrium. That is, the sum of the forces on the parachute is equal to zero. Forces acting on a parachute are shown in Fig. 1.
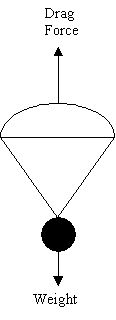
Figure 1
Weight (W) acts downward, through the center of mass. The resistance of the ambient air creates a drag force D. These forces are balanced once terminal velocity is reached.
W = D
Weight
Weight is given by W = mg, where m is the mass of the payload plus the mass of the parachute.
Drag
Drag force is the retarding force acting upon a body as it moves through a fluid. Engineers commonly predict drag using.
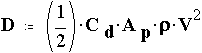
where Cd, the coefficient of drag, is found from experiments. Values for a parachute are 0.8 < Cd < 1.2. Note that Cd is unitless.
The term Ap is the projected area of the object. Imagine shining a light directly on an object. The surface area of the shadow equals projected area. Thus, for a hemisphere, the projected area equals the area of circle of radius r.
Calculation of radius for a Parachute
To find the radius of a parachute, we equate weight with drag:
![]()
Using the drag formula gives
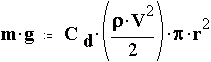
Solving for radius gives
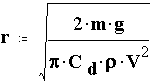
Example
Given an object of mass m = 100 g, find the radius of parachute needed to provide a terminal velocity of V = 7.5 m/sec. Assume Cd = 1.2
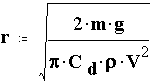
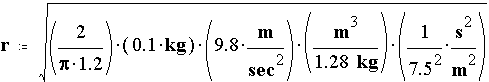
![]()
Note that this radius corresponds to the parachute as a three-dimensional object. If one was to cut a round parachute out of a sheet of plastic, the radius of the plastic would need to be larger than this value.